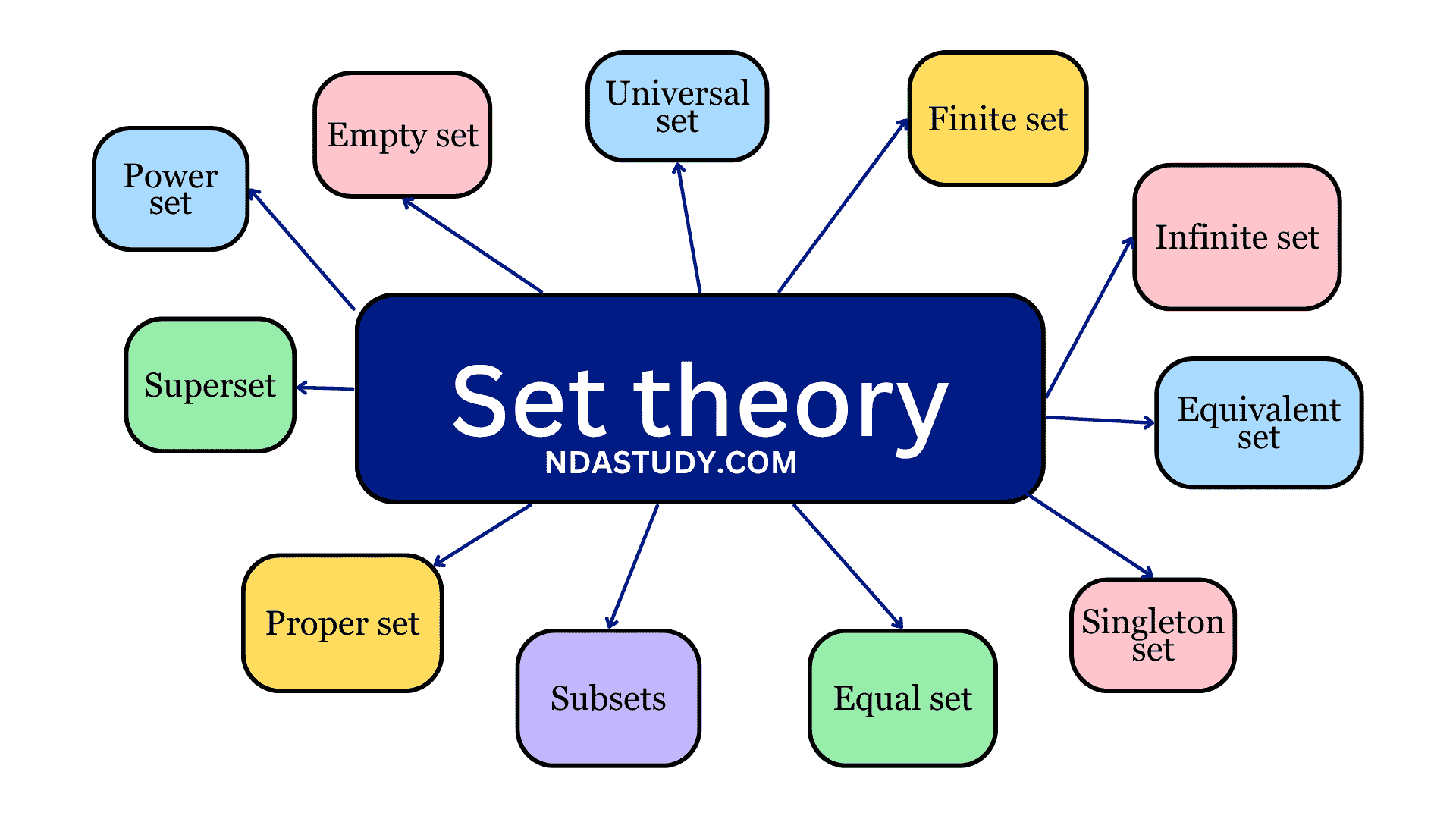
Types of set: Empty set, subsets, power set & more

Types of set/set theory A set is a well-defined collection of objects/elements. According to its properties and characteristics, the Set can be divided into many types. Types of set are:-

Empty set: Types of sets

It is a types of set or A set that does not contain any elements is called the empty set. It is also called the void or the null set and represented by {} or Ø. For example,

• A = {x:x is a student presently studying in both classes 11 and 12}=Ø; we know that a student cannot study simultaneously in both classes 11 and 12.
• B = {x:6<x<8, x is a even natural number}, x∉B and 7 is not a even natural number.
• C = {x:x is an even prime number greater than 2}=Ø and 2 is only even prime number.

Singleton set: Types of sets

It is a types of set that contains only one element or if the cardinality of a Set is one(1). For example,

• A = {x:x is an even prime number},i.e., |A|=1
• B = {x:20<x<28, x is a prime number}, i.e., o(B)=n(B)=|B|=1

NOTE:- Empty sets are not singleton sets, Because a singleton set contains one(1) element But, an empty set contains no elements or zero elements.

Finite set: Types of sets

A set that is either an Empty set or contains a definite number of elements. For example,

• W = {x:x is the days of the week}.
• P = {x:x∈N and 2x-1=0}, |P|=0 or P is an empty set. Therefore it is a finite set.

Infinite set: Types of sets

A Set that contains infinite elements/objects. For example,

• P: The set of all points on a line.
• N = {1,2,3,4,5,…..}
• Z = {…..,-3,-2,-1,0,1,2,3,…..}

Equivalent sets:

NDA Eligibility for Female 2023: Height, Age Limit, Qualification!

Types of sets

when the cardinal number of two Sets is the same. For example,

• A = {1,2,3} and B = {a,b,c}, Both the sets are equivalent set; n(A)=3=n(B).
• C = {t, a,n} and D = {a,n,t}; n(C)=3=n(D).

Equal set:

When the elements and the number of Elements or two Sets are the same. For example,

• C = {t,a,n} and D = {a,n,t}; C=D.

NOTE:- If two sets are not equal (i.e., let A ={a,n,d}), then they both are Unequal sets and written as A≠C
Every equal set is equivalent, but every equivalent set may not be an Equal set,i.e., above set C and D is an Equal set, and their cardinal number is the same, so set C and D is also an equivalent set. Now if we take the example of Set A and B, |A|=3 and |B|=3; but, A = {1,2,3}≠{a,b,c}=B

Subsets:

Set A is a subset of B “iff” or if and only all the elements of Set A are also the elements of Set B or Contained in Set B. Symbol of a subset is ⊆ or ⊂.

• A = {all the cadets of NDA} and B = {all the cadets of the first semester of NDA}; B⊂A and read as B is a subset of A or Contained in A.
• C = {N,D,A} and D = {D,N,A}; C⊆D or D⊆C.

NOTE:- 

1. If Set C is a subset of D and Set D is a subset of C (C⊆D and D⊆C), Then Sets C and D are equal sets or C=D and vice-versa.
2. Ø or {} is a subset of every set.
3. Every set is a subset of itself.
4. The number of subsets of A = 2^n(A), where n(A) = Order/cardinality or number of elements in set A. Let set A = {1,2,3}; here n(A)=3 and 2^n(A)= 23 = 8 are – {1},{2},{3},{1,2},{1,3},{2,3},{1,2,3},{}.

Proper set and Superset: 

Let P and S be two sets. If P⊂S and P≠S, Then P is called a proper subset of S, and S is called a superset of P. Symbols of Proper set is ⊂ not ⊆. Examples are,

• A = {2,4,6,8,10} is proper subset of B ={1,2,3,4,5,6,7,8,9,10}.
• B = {1,2,3,4,5,6,7,8,9,10} is superset of C = {1,3,5,7,9}.

Power set:

 The collection of all subsets of a Set is called the Power set of the set. Let A be a set, then the power set of A is denoted by P(A). In P(A), every element is a set. For example,

•  if P(A)={1,2,3}, then P(A)={Ø,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}} and n[P(A)]=2^3=8.

Universal set: 

A set that contains every element of all the Sets under consideration, including some other Elements. (denoted by U). For example,

• A = {1,2,3}, B = {2,4,6,8} and C = {1,3,5,7,9}, therefore, U = {1,2,3,4,5,6,7,8,9}.
• [Read sets theory in detail]

For more Contact @NDAstudyOfficial or @NDAstudy